Hopf-Rinow II and an application November 15, 2009
Posted by Akhil Mathew in differential geometry, MaBloWriMo.Tags: geodesic completeness, geodesics, homotopy, Hopf-Rinow theorem, Riemannian manifolds
2 comments
Now, let’s finish the proof of the Hopf-Rinow theorem (the first one) started yesterday. We need to show that given a Riemannian manifold which is a metric space
, the existence of arbitrary geodesics from
implies that
is complete with respect to
. Actually, this is slightly stronger than what H-R states: geodesic completeness at one point
implies completeness.
The first thing to notice is that is smooth by the global smoothness theorem and the assumption that arbitrary geodesics from
exist. Moreover, it is surjective by the second Hopf-Rinow theorem.
Now fix a -Cauchy sequence
. We will show that it converges. Draw minimal geodesics
travelling at unit speed with
The Hopf-Rinow theorems and geodesic completeness November 14, 2009
Posted by Akhil Mathew in differential geometry, MaBloWriMo.Tags: completeness, geodesic completeness, geodesics, Hopf-Rinow theorem, Riemannian manifolds
10 comments
Ok, yesterday I covered the basic fact that given a Riemannian manifold , the geodesics on
(with respect to the Levi-Civita connection) locally minimize length. Today I will talk about the phenomenon of “geodesic completeness.”
Henceforth, all manifolds are assumed connected.
The first basic remark to make is the following. If is a piecewise
-path between
and has the smallest length among piecewise
paths, then
is, up to reparametrization, a geodesic (in particular smooth). The way to see this is to pick
very close to each other, so that
is contained in a neighborhood of
satisfying the conditions of yesterday’s theorem; then
must be length-minimizing, so it is a geodesic. We thus see that
is locally a geodesic, hence globally.
Say that is geodesically complete if
can be defined on all of
; in other words, a geodesic
can be continued to
. The name is justified by the following theorem:
Theorem 1 (Hopf-Rinow)
The following are equivalent:
is geodesically complete.
- In the metric
on
induced by
(see here),
is a complete metric space (more…)
Geodesics are locally length-minimizing November 13, 2009
Posted by Akhil Mathew in differential geometry, MaBloWriMo.Tags: Gauss lemma, geodesics, Riemannian manifolds
add a comment
Fix a Riemannian manifold with metric and Levi-Civita connection
. Then we can talk about geodesics on
with respect to
. We can also talk about the length of a piecewise smooth curve
as
Our main goal today is:
Theorem 1 Given
, there is a neighborhood
containing
such that geodesics from
to every point of
exist and also such that given a path
inside
from
to
, we have
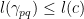
with equality holding if and only if
is a reparametrization of
.
In other words, geodesics are locally path-minimizing. Not necessarily globally–a great circle is a geodesic on a sphere with the Riemannian metric coming from the embedding in , but it need not be the shortest path between two points. (more…)