The torsion tensor and symmetric connections

The torsion tensor and symmetric connections November 8, 2009

Posted by Akhil Mathew in differential geometry, MaBloWriMo.
Tags: connections, symmetric connections, torsion tensor
trackback

Today I will discuss the torsion tensor of a Koszul connection. It measures the deviation from being symmetric in a sense defined below.

Torsion

Given a Koszul connection ${\nabla}$ on the smooth manifold ${M}$ , define the torsion tensor ${T}$ by

$\displaystyle T(X,Y) := \nabla_X Y - \nabla_Y X - [X,Y].$

It can be checked that ${T}$ is a tensor, using the identities for ${\nabla}$ and those for the Lie bracket. For instance, here is the proof that ${T(fX,Y)=fT(X,Y)}$ for a smooth ${f}$ .

$\displaystyle T(fX,Y) = \nabla_{fX}Y - \nabla_Y(fX) - [fX,Y].$

In view of the connection identities and ${[fX,Y] = f(X \circ Y) - Y \circ (f X) = f(X \circ Y - Y \circ X) - (Yf)X}$ , we get that this equals

$\displaystyle f \nabla_X Y - f \nabla_Y X - (Yf) X - f[X,Y] + (Yf)X = fT(X,Y) .$

When ${T \equiv 0}$ , we call ${\nabla}$ symmetric. There is a useful motivation for this terminology: when we are in an open subset of ${\mathbb{R}^n}$ , the condition is equivalent to ${T\left( \partial_i, \partial_j\right)=\nabla_{\partial_i} \partial_j - \nabla_{\partial_j} \partial_i = 0}$ for all ${i,j}$ , or equivalently

$\displaystyle \Gamma^k_{ij} = \Gamma^k_{ji},$

where the ${\Gamma_{ij}^k}$ are the Christoffel symbols.

Vector fields along a surface

There is a useful consequence of symmetry that I will now discuss. If ${s: U \rightarrow M}$ where ${U \subset \mathbb{R}^2}$ is open, then we can call ${s}$ a surface. We can define a vector field along ${s}$ in the same way as a vector field along a curve—it is a smooth map ${V: U \rightarrow TM}$ with ${V}$ projecting down to ${s}$ .

One way to get a vector field along ${s}$ is to consider the partial derivatives ${\frac{\partial}{\partial x} s, \frac{\partial}{\partial y} s}$ . Equivalently, these are obtained by ${s_*\left( \frac{\partial}{\partial x} \right), s_{*}\left(\frac{\partial}{\partial y} \right)}$ .

Given a vector field ${V}$ along ${s}$ , we can consider the “partial covariant derivatives” ${\frac{D}{\partial x} V, \frac{D}{\partial y} V}$ defined respectively at ${(x,y)}$ as the covariant derivative of the vector field along a curve ${x \rightarrow V(x,y)}$ or ${y \rightarrow V(x,y)}$ . These are also vector fields along ${s}$ . It can be checked that these operations preserve smoothness.

Another way to think of this is ${\frac{D}{\partial x} V = \nabla_{s_*\left( \frac{\partial}{\partial x} \right)} V}$ , and similarly for ${y}$ . There is a slight abuse of notation because ${V}$ is only a vector field along ${s}$ , but at least when ${s}$ is an immersion this is ok because you can locally extend vector fields along ${s}$ .

Here is a useful consequence of symmetry.

Proposition 1

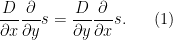
Let ${s}$ be a surface in ${M}$ , and let ${\nabla}$ be a symmetric connection on ${M}$ . Then $\displaystyle \frac{D}{\partial x} \frac{\partial}{\partial y} s = \frac{D}{\partial y} \frac{\partial}{\partial x} s.\ \ \ \ \ (1)$

So symmetry is just a version of Clairaut’s theorem.

One way to prove this is to compute in a coordinate system.

The following argument is incorrect. I will post a corrected proof later today.

Another, more conceptual way, to argue is as follows. Given an embedding ${i: N \rightarrow M}$ , we can obtain a connection ${\nabla'}$ on ${M}$ by defining

$\displaystyle \nabla'_{X} Y := \nabla_{i_* X} i_* Y.$

Of course, there is some checking to be done here. ${i_* X,i_* Y}$ aren’t really vector fields, but one can check (as with the definition of the covariant derivative) that it doesn’t matter, because you just extend them locally to vector fields. Then if ${X',Y' \in \Gamma(N)}$ are ${i}$ -related to ${X,Y \in \Gamma(M)}$ , it follows that

$\displaystyle T(X',Y') \ \mathrm{is \ } i-\mathrm{related \ to} \ T(X,Y).$

Consider an immersion ${s: U \rightarrow M}$ for ${U \subset \mathbb{R}^2}$ open. Then

$\displaystyle \frac{D}{\partial x} \frac{\partial}{\partial y} s = \nabla_{s_{*} \left( \frac{\partial}{\partial x} \right) } s_{*}\left( \frac{\partial}{\partial y} \right) = \nabla_{s_{*} \left( \frac{\partial}{\partial y} \right) } s_{*}\left( \frac{\partial}{\partial x} \right) - s_{*} T'\left( \frac{\partial}{\partial x}, \frac{\partial}{\partial y} \right).$

Now ${\nabla'}$ is symmetric, so ${T'=0}$ and this turns into

$\displaystyle \nabla_{s_{*} \left( \frac{\partial}{\partial y} \right) } s_{*}\left( \frac{\partial}{\partial x} \right) = \frac{D}{\partial y} \frac{\partial}{\partial x} s.$

We’ve now handled the case of ${s}$ an immersion. Now consider the general case. Fix an arbitrary ${s: U \rightarrow M}$ with ${p \in U}$ , and consider the two quantities in (1) at ${p}$ . If we choose an immersion ${t: D_r(p) \rightarrow M}$ where ${r}$ is very small (possible if ${\dim M \geq 2}$ , which we can assume), then ${s + \epsilon t}$ is an immersion at ${p}$ if ${\epsilon}$ is very small. Thus

$\displaystyle \frac{D}{\partial x} \frac{\partial}{\partial y} ( s + \epsilon t) = \frac{D}{\partial y} \frac{\partial}{\partial x} ( s + \epsilon t)$

at ${p}$ , at least. Letting ${\epsilon \rightarrow 0}$ , the two quantities are equal.

So what’s next? First, I ought to do something like this for the curvature tensor, though it’ll go a bit more quickly since the pattern is similar. Then, I should talk about the Levi-Civita connection associated to a Riemannian metric and how geodesics turn out to be locally distance-minimizing paths. This will provide ample material for a couple of more posts, and then I have other differential geometry topics in mind.

Comments»

1. Evolution Gaming - September 26, 2023: Evolution Gaming

The torsion tensor and symmetric connections | Delta Epsilons

Reply

	Evolution Gaming on The torsion tensor and symmetr…
	Proof that a group r… on Basics of group representation…
	Jahnke on The Hahn-Banach theorem and tw…
	pageanu on Some unsolved problems
	Ingo Blechschmidt on Generic freeness II

Delta Epsilons