The Hahn-Banach theorem and two applications

The Hahn-Banach theorem and two applications November 28, 2009

Posted by Akhil Mathew in analysis, functional analysis, MaBloWriMo.
Tags: convex sets, Hahn-Banach theorem, hyperplane separation theorem, linear functionals, Muntz approximation theorem
trackback

I have been finishing my MaBloWriMo series on differential geometry with a proof of the Myers comparison theorem, which right now has only an outline, but will rely on the second variation formula for the energy integral. After that, it looks like I’ll be posting somewhat more randomly. Here I will try something different.

The Hahn-Banach theorem is a basic result in functional analysis, which simply states that one can extend a linear function from a subspace while preserving certain bounds, but whose applications are quite manifold.

Edit (12/5): This material doesn’t look so great on WordPress. So, here’s the PDF version. Note that the figure is omitted in the file.

The Hahn-Banach theorem

Theorem 1 (Hahn-Banach) Let ${X}$ be a vector space, ${g: X \rightarrow \mathbb{R}_{\geq 0}}$ a positive homogeneous (i.e. ${g(tx) = tg(x), t >0}$ ) and sublinear (i.e. ${g(x+y) \leq g(x) + g(y)}$ ) function.

Suppose ${Y}$ is a subspace and ${\lambda: Y \rightarrow \mathbb{R}}$ is a linear function with ${\lambda(y) \leq g(y)}$ for all ${y \in Y}$ .

Then there is an extension of ${\lambda}$ to a functional ${\tilde{\lambda}: X \rightarrow \mathbb{R}}$ with

$\displaystyle \tilde{\lambda}(x) \leq g(x), \ x \in X.$

I’ll omit the proof; I want to discuss why it is so interesting. One of its applications lies in questions of the form “are elements of this form dense in the space”? The reason is that if ${X}$ is a normed linear space and ${Y}$ a closed subspace, the quotient vector space ${X/Y}$ is a norm with the norm ${|x+Y| := \inf_{y\in Y} |x-y|.}$ (The closedness condition is necessary because otherwise there might be nonzero elements of ${X/Y}$ with zero norm.) So:

Corollary 2 Let ${X}$ be a normed linear space, ${Y}$ a subspace. Then ${x \in \bar{Y}}$ if and only if: Every bounded linear functional ${\lambda: X \rightarrow \mathbb{R}}$ vanishing on ${Y}$ vanishes on ${x}$ .

One implication is immediate; linear functionals are continuous. For the other, note that the condition is equivalent to “any bounded linear functional ${\lambda}$ on ${X/\bar{Y}}$ satisfies ${\lambda(\bar{x})=0}$ , where ${\bar{x}}$ denotes the image of ${x}$ .”In particular, we are reduced to showing that if ${Z}$ is a normed linear space ${z \in Z}$ is nonzero, there is a bounded linear functional that does not annihilate ${z}$ . To do this, we apply the Hahn-Banach theorem to ${Z}$ and the subspace ${\mathbb{R}.z}$ , with ${g}$ as some multiple of the norm. Choose any nonzero linear functional on this subspace, and then extend to all of ${Z}$ .

An approximation result for powers of ${t}$ A spectacular application of this is the following:

Theorem 3 (Muntz) If ${\{\lambda_n\}}$ is a sequence of positive real numbers with ${\sum \lambda_n^{-1} = \infty}$ , then the linear combinations of the functions ${t^{\lambda_n}}$ are dense in ${C([0,1])}$ , the space of real continuous functions on the unit interval with the sup norm.

The proof starts by employing the above corollary: for a sequence ${\{\lambda_n\}}$ with the powers ${\{t^{\lambda_n}\}}$ not dense in ${C(0,1)}$ , there is a nonzero continouus functional ${\lambda: C([0,1]) \rightarrow \mathbb{R}}$ with $\displaystyle \lambda(t^{\lambda_n}) = 0, \ \forall n.$ The elegant idea in this proof is to consider the complex function $\displaystyle F(z) := \lambda( t^z ) = \lambda(Re(t^z)) + i \lambda(Im(t^z))$ defined in the right half-plane ${Re(z)>0}$ . This is an analytic function in ${z}$ , because $\displaystyle \frac{ F(z+\eta)-F(z)}{\eta} = \lambda\left( \frac{t^{z+\eta} - t^z}{\eta} \right).$ When ${Re(z)>0}$ , the function ${\frac{t^{z+\eta} - t^z}{\eta}}$ tends uniformly in ${t}$ (in the unit interval) to ${(\log t) t^z}$ .These are the basic properties of ${F}$ :

${||F||_{\infty} < \infty}$ . Indeed, ${\lambda}$ is a bounded functional and the function ${t^z}$ has norm 1.
${F(n) \not\equiv 0}$ . Indeed, otherwise ${F(n)=0}$ for ${n \in \mathbb{N}}$ , implying ${\lambda}$ vanishes on polynomials. But the Weierstrass theorem implies these are dense in ${C(0,1)}$ , so ${\lambda \equiv 0}$ , contradiction.

There are general theorems characterizing the roots of a bounded analytic function in some disk (in some, boundedness can be weakened to a ${H^p}$ condition). Since the right half-plane is conformally equivalent to the disk via the transformation $\displaystyle \phi: z \rightarrow \frac{z-1}{z+1}$ we can consider the bounded analytic function ${F \circ \phi^{-1}}$ on the unit disk, which has roots at $\displaystyle \frac{\lambda_n - 1}{\lambda_n+1}.$ Now I quote the following theorem:

Theorem 4 Let ${f : U \rightarrow \mathbb{C}}$ be a bounded analytic function. If the zeros of ${f}$ in ${U}$ are ${\zeta_n}$ , then $\displaystyle \sum (1 - |\zeta_n|) < \infty.$

This can be proved using Blaschke products; see Rudin’s Real and Complex Analysis.So for our function ${F \circ \phi^{-1}}$ , we find $\displaystyle \sum \left( 1- \frac{\lambda_n - 1}{\lambda_n+1} \right) = \sum \frac{2}{\lambda_n + 1} < \infty,$ which shows that ${\sum \lambda_n^{-1} < \infty}$ , and which proves the theorem.It’s in fact true that the condition is necessary, and the ${\lambda_n}$ can be made complex. Cf. Rudin.

Geometric applications Let ${C}$ be a closed convex plane region, and ${p \in \partial C}$ :Then there exists a line through ${p}$ such that ${C}$ lies on one side of ${p}$ —i.e., a support line. This can be proven using a bit of elementary geometry, but it also follows from fancier arguments as well.Basically, the assertion of the theorem can be rephrased as follows: the line corresponds to a linear functional ${\lambda: \mathbb{R}^2 \rightarrow \mathbb{R}}$ , such that ${\lambda(p) = c}$ and ${\lambda(A) \subset (-\infty, c]}$ .

Theorem 5 Let ${A}$ , ${B}$ be disjoint convex sets in a topological vector space such that ${A}$ contains an interior point. Then there is a nonzero continuous linear functional ${\lambda : X \rightarrow\mathbb{R}}$ with $\displaystyle \sup_{a \in A} \lambda(a) \leq \inf_{b \in B}\lambda(b).$

The geometric fact above follows from taking ${B = p}$ , ${C = Int(A)}$ .For a convex set ${C}$ , we define the Minkowski functional $\displaystyle g_C(x) = \inf \{ t^{-1} : t > 0, tx \in C \}.$ Then:

${g_C}$ is positive homogeneous—this is evident.
${g_C(x+y) \leq g_C(x)+g_C(y)}$ . Indeed, if ${t^{-1}x \in C, u^{-1}y \in C}$ , then $\displaystyle (x+y) = \frac{t}{t+u} (t^{-1}x ) + \frac{u}{t+u} (u^{-1}y) \in C$ by convexity. So ${(t+u)^{-1}(x+y) \in C}$ , which proves subadditivity.

If ${C}$ has an interior point at zero, ${g_C}$ is always finite.Now consider ${A-B:=\{ a-b, a \in A, b \in B\}}$ . This is a convex set, and I will show that there is a continuous functional ${\lambda}$ with ${\lambda(A-B) \subset (-\infty.0]}$ , which will prove the theorem.Choose ${x_0 \in A-B}$ and consider the set ${C := A-B - x_0 = (A-B)-x_0}$ ; if ${x_0}$ is chosen appropriately, this will contain a neighborhood of ${0}$ . Now ${g_C(-x_0) \geq 1}$ (since otherwise ${-x_0 \in C}$ and ${A \cap B \neq \emptyset}$ ). There is a linear functional ${\lambda: \mathbb{R}x_0 \rightarrow \mathbb{R}}$ with ${\lambda(-x_0)=1}$ bounded by ${g_C}$ (this is seen for ${-tx_0}$ with ${t\geq0}$ by positive homogeneity; for ${tx_0}$ with ${t >0}$ , ${\lambda}$ is negative), which we can extend to all of ${X}$ with the same bound. Then $\displaystyle \lambda(A-B) \subset -1 + \lambda(C) \leq -1 + g_C(C) \leq 0,$ where I have abused notation by writing ${E \geq F}$ for ${E,F \subset \mathbb{R}}$ when every element of ${E}$ is greater than or equal to every element of ${F}$ .

Corollary 6 If ${A,B}$ are closed convex subsets of a locally convex space ${X}$ , we can get a nonzero continuous ${\lambda \in X^*}$ as above with even $\displaystyle \lambda(a) < \lambda(b)$ if ${a \in A, b \in B}$ .

Indeed, we can find a small convex neighborhood ${U}$ of the origin such that ${A+U, B}$ are disjoint. Then apply the above result to ${A+U, B}$ and note that ${\lambda(U) \neq 0}$ .

Comments»

1. chandrasekhar - September 29, 2011: Dear Akhil,

Do you think that positive homogenous condition is really required? Because Aliprantis in his book “Principles of real analysis” does mention that condition.

Reply
2. chandrasekhar - September 29, 2011: Oops, I made a mistake. He assume that by sublinear he means:

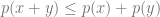
– $p(x+y) \leq p(x)+p(y)$

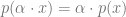
– $p(\alpha \cdot x) = \alpha \cdot p(x)$

Reply
3. chandrasekhar - September 29, 2011: Hey Muntz’s theorem is really powerful and surprising. Thanks for the post.

Reply
4. Konstantinos - April 29, 2012: Reblogged this on Room 196, Hilbert's Hotel and commented:
I’ve been studying the Hahn – Banach theorem and I found this post very informative! 😀

Reply
5. Advanced Analysis, Notes 6: Banach spaces (basics, the Hahn-Banach Theorems) « Noncommutative Analysis - November 2, 2012: […] polynomials in prime powers of are dense in , isn’t that neat? See Theorem 3 on this post for the part of the proof of Muntz’ theorem (the sufficiency part – which is the more […]

Reply
6. Jahnke - May 17, 2019: In “Geometric applications ” your picture is not convex. Please, fix it.

Reply

	Evolution Gaming on The torsion tensor and symmetr…
	Proof that a group r… on Basics of group representation…
	Jahnke on The Hahn-Banach theorem and tw…
	pageanu on Some unsolved problems
	Ingo Blechschmidt on Generic freeness II

Delta Epsilons